1. 신경망 층
신경망의 층은 다음과 같이 입력층, 은닉층, 출력층으로 나누어진다.

1) 입력층 (Input Layer)
데이터를 입력받는 층이며, 어떠한 연산도 일어나지 않는다. 노드의 수는 입력 변수의 수와 같으며, 신경망의 깊으를 셀 때 입력층은 포함하지 않는다.
2) 은닉층 (Hidden Layer)
입력층과 출력층을 제외한 모든 층을 말한다. 사용자는 입력층과 출력층만 볼 수 있으며 은닉층의 연산 결과를 볼 수 없다. 은닉층의 노드 개수는 하이퍼 파라미터이며, 노드 수가 많아지면 다양한 파라미터를 학습할 수 있어 정확도가 올라가지만 학습 시간이 늘어나고 오버피팅 가능성이 높아진다.
3) 출력층 (Output Layer)
가장 마지막 출력층이다. 분류 문제의 경우 출력층에 활성함수(Activation Function)가 존재한다. 이진 분류의 경우 Sigmoid 함수를 활성함수로 사용하며, 다중 클래스 분류 문제에서는 Softmax를 활성함수로 사용한다. 복잡한 딥러닝 방법론에서는 은닉층에서도 활성함수를 사용한다.
2. Activation Function
2-1) Sigmoid 함수

* Sigmoid 함수의 문제점
가중치 학습 과정은 다음과 같다. Input 값이 들어오면, W를 곱하고 Sigmoid를 활성화 함수로 활용하여 Output을 출력한다. 이 때, Loss Function을 통해 Output과 실제 데이터간의 차이인 Loss 값을 구하고 이를 미분하여 Gradient값을 구한다. 구해진 Gradient값을 역전파 알고리즘을 통해 앞단으로 전파하며 가중치를 업데이트 한다.
이 때, sigmoid의 양 끝값에서 Gradient값은 0에 매우 가까운 값이 나온다. Activation Funcion에서 Gradient가 곱해지는 과정에서, 뒷단에서 Loss로부터 전파되는 Gradient는 앞단으로 가면서 소멸된다. 이러한 현상을 Vanishing Gradient라고 한다.


2-2) ReLU
이러한 현상을 해결하기 위해 도입된 활성화 함수가 ReLU이다. ReLU는 어떠한 값이 들어왔을 때 해당 값이 0보다 작으면 0을, 그렇지 않으면 자기 자신을 return한다. 따라서 0보다 큰 값에서는 Gradient가 1이 되며, 이를 통해 Gradient Vanishing을 해결한다. 하지만, 음수 영역에서는 Gradient가 0이기 때문에 Gradient가 사라진다는 문제가 있긴 하지만, 큰 문제가 되지는 않는다고 한다. 이러한 문제점을 해결한 Activation Function이 leaky_relu이다.

2-3) 기타 Activation Function
각각 활성 함수마다의 특징과 장단점이 있으니 데이터의 특성 및 예측하고자 하는 Output의 Type에 따라 잘 선택해서 사용하면 될 것 같다.

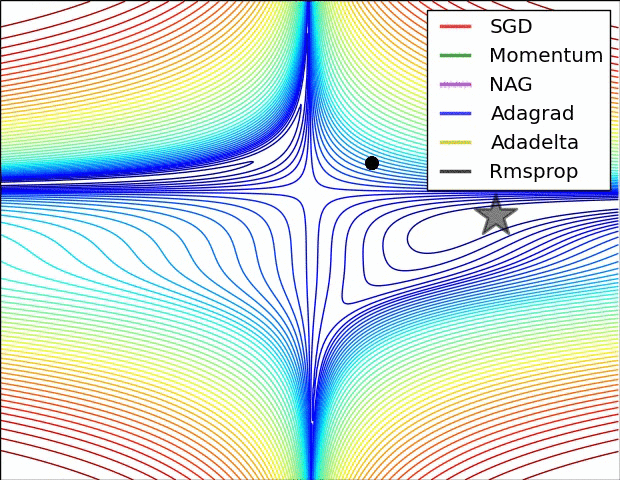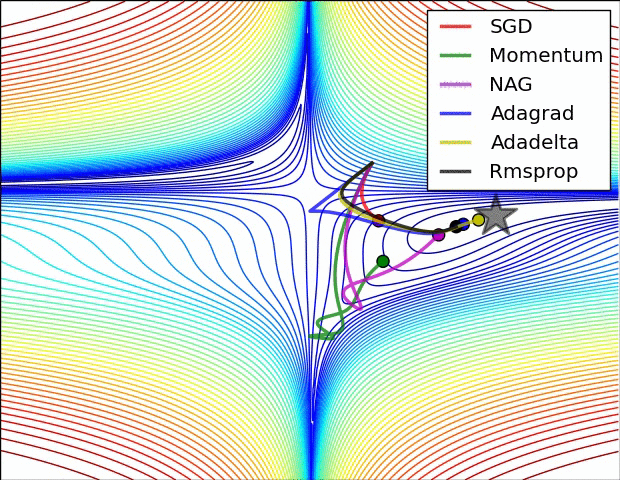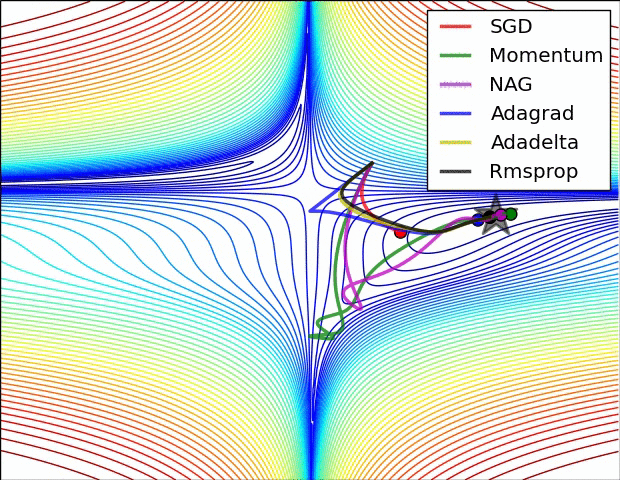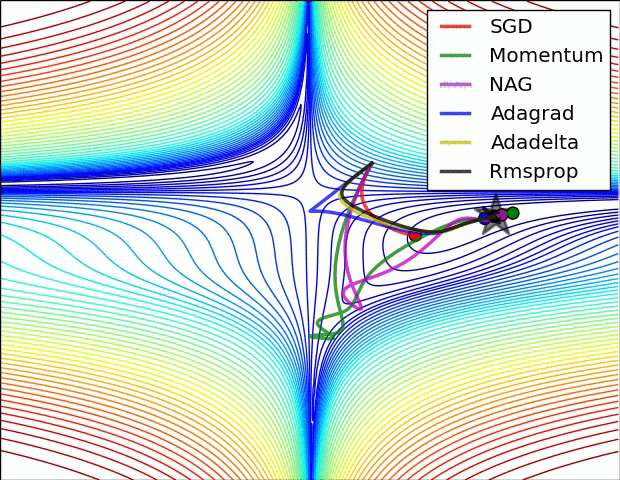
3. Optimizer
Loss Function은 실제값과 예측값간의 차이를 나타낸다. 이러한 손실함수를 최소화 하는것이 최적화(Optimization)이며, 이를 수행하는 알고리즘이 최적화 알고리즘(Optimizer)이다. 손실함수를 줄여나가면서 학습하는 방법은 어떤 optimizer를 사용하느냐에 따라 달라진다. 현재 딥러닝 모델에서 가장 많이 사용하는 Optimizer는 Adam이며, Momentum과 RMSProp을 결합한 형태로 각 파라미터마다 다른 크기의 업데이트를 적용한다.

Reference
댓글남기기