CNN
1. Fully Connected Layer
FC Layer는, input 이미지를 1차원으로 쭉 펴서 Weight와 곱해주는 Layer이다. 가령, 32x32x3의 input image가 있다면, FC Layer는 이를 3072x1의 벡터로 쭉 핀 다음 W와 내적을 하여 activation map을 얻는다. 가장 간단하게 생각할 수 있는 layer이긴 하지만, Fully Connected Layer에는 치명적인 단점이 2가지 존재한다.

-
이미지의 지역적 정보 반영x
이미지를 1차원으로 펴서 사용하기 떄문에, 이미지의 지역적인 정보가 사라진다는 단점이 존재한다.
-
Overfitting
class가 많아질 경우, overfitting 문제가 발생하기 쉽다고 한다.
2. Convolutional Layer

FC Layer가 input image를 쭉 펴서 연산하였다면, Conv Layer는 기존의 이미지 구조를 그대로 유지한 채 연산한다. CNN에서는 가중치를 필터라고 부르는데, 이 작은 필터가(예시에서는 5x5x3 필터) 이미지를 슬라이딩 하며 공간적으로 내적을 수행하게 된다. Conv Layer는 input 이미지의 구조를 그대로 유지한 채 필터가 움직이며 연산을 하므로, 이미지의 지역적 정보가 보존된다.

CNN은 이런식의 convolutional layer들이 연속된 형태이며, 입력 이미지는 이 Layer들을 차례로 통과한다. 그 사이사이에 ReLU와 같은 non-linaer layer(activation function)를 넣어, conv-ReLU가 반복되는 구조이며, 이미지 크기 조정을 위해 중간중간 Pooling Layer가 추가된다. 각 layer의 출력은 다음 layer의 input이 되어 뒷단으로 계속 전파되며, 제일 끝단의 FC-Layer가 정답 클래스에 맞게 1차원 벡터로 펴준다.
2-1) Filter
필터는 CNN에서 사용하는 가중치로서, input image에서 특정 feature를 추출하는 역할을 한다. 하나의 필터를 가지고 input 이미지에 convolution을 수행하여 나온 출력값을 activation map이라고 하는데, 이 activation map들이 다음 Layer의 input으로 들어가 계속 뒷단으로 전파된다. 이게 CNN의 핵심 아이디어다. (중간에 Activation Function, Pooling Layer도 있긴 하지만, 해당 내용은 차후에 차차 소개하겠다.)


2-1-1) 연산
Filter는 이미지의 좌상단부터 시작하여, 내적을 수행하게 된다. 여기서 나온 값(단일 스칼라 값)은, 다시 output activation map의 해당 위치에 저장된다. 그리고 다시 옆으로 슬라이딩하여 위 과정을 반복한다. 이 때, 슬라이딩하는 거리나 필터의 크기에 따라서 activation map의 크기가 달라진다(activation map의 크기를 계산하는 방법은 이후에 설명한다). 이는 하이퍼 파라미터로, 데이터의 크기나 상황등에 따라 잘 조정해야한다.
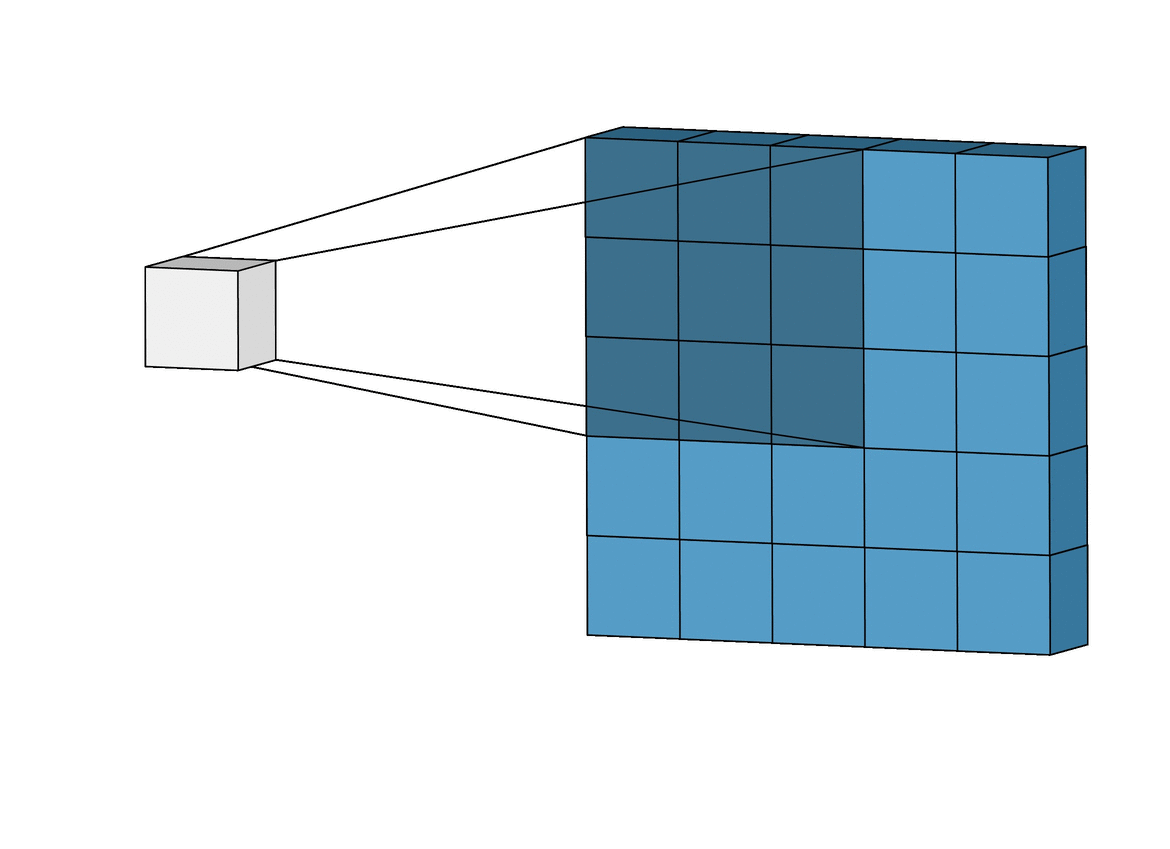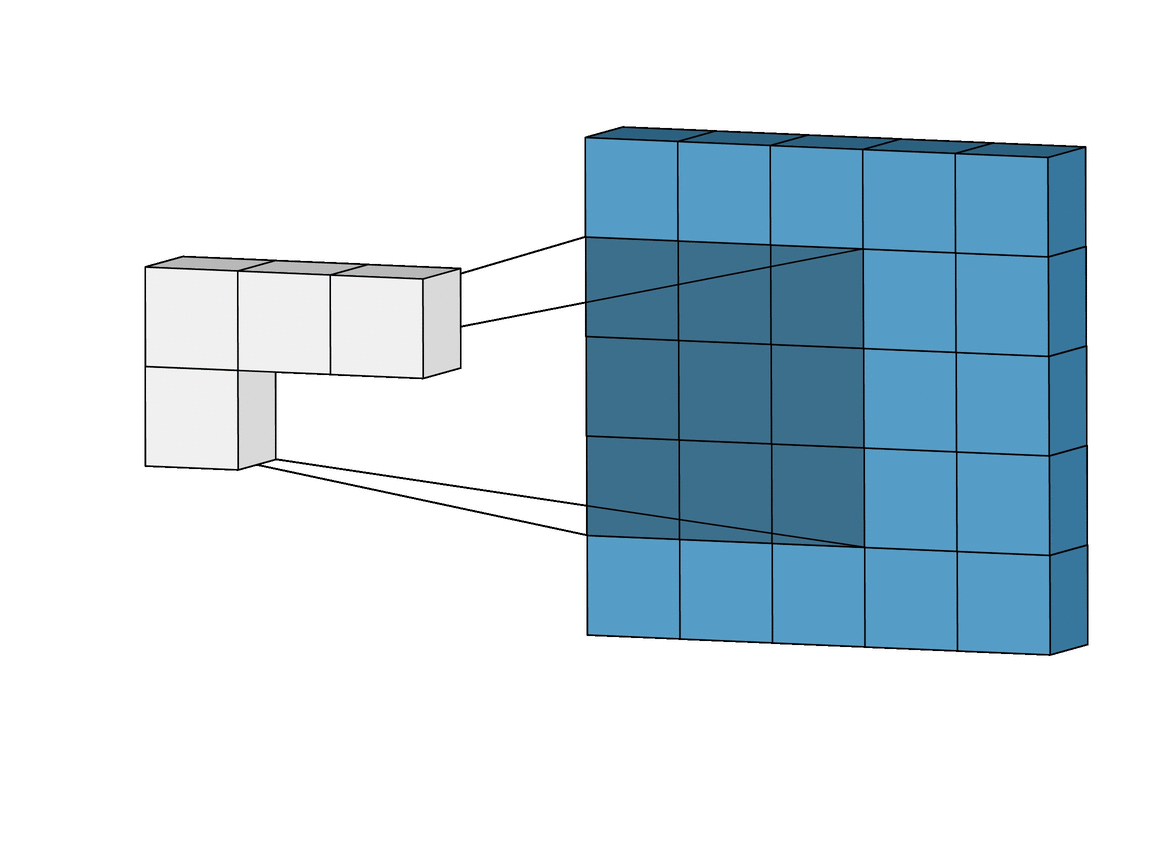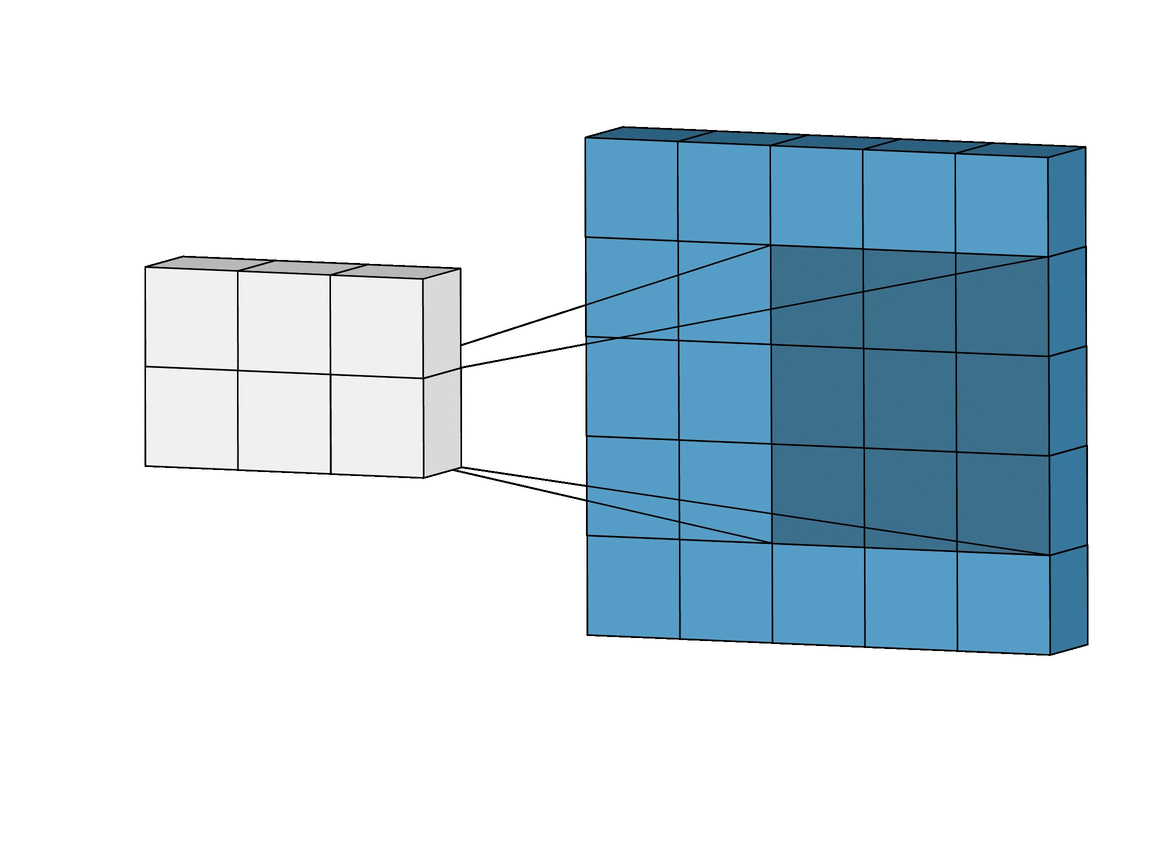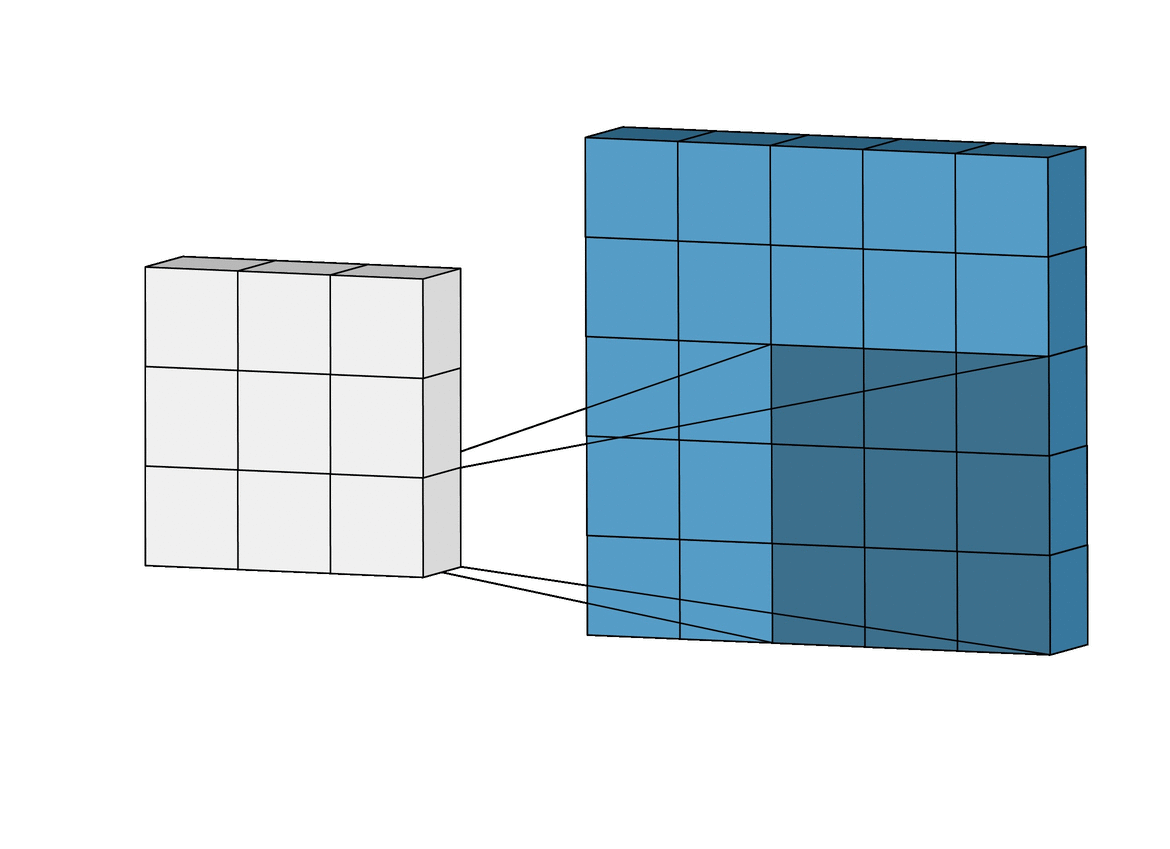
2-1-2) Depth
하나의 필터는 input 이미지의 아주 작은 부분을 취하며(32x32 중 3x3, 5x5 등), depth는 input image의 depth를 따른다. 아래 그림과 같이 input image의 채널이 RGB 3채널이라면, filter의 depth도 3이되어 각각의 채널에서 연산을 진행한다.

2-1-3) 필터의 개수
또한, 보통 convolution layer에서는 여러개의 필터를 사용한다. 왜냐하면, 이미지마다 여러가지의 특징이 있을 수 있는데(ex. 고양이: 뾰족한 귀, 털, 꼬리 등등), 이러한 이미지 특성을 고려하여 다양한 필터로 다양한 특징을 추출하고 싶기 때문이다. 이렇게 되면, 각 필터마다 1개의 activation map이 추출되어, 최종적으로 필터의 총 개수만큼 activation map이 추출된다. 따라서 output activation map의 채널은 필터의 개수와 동일하다.

2-1-4) Stride
만약, 다음과 같은 7x7 이미지에 3x3 필터를 적용한다고 해보자.

filter는 다음과 같은 process로 activation map을 얻게 될 것이다.
좌측 상단에서 시작 -> 필터를 씌우고, 해당 값들의 내적을 수행 -> 결과값은 activation map의 좌상단에 위치 -> 값하나 얻기 -> 필터를 오른쪽으로 n칸 움직임 -> 반복...
여기서 filter가 움직이는 칸의 수를 지정할 수 있는데, 이를 stride라고 한다.
-
Stride = 1
stride가 1인 경우, 위 process를 계속 반복하면 상하좌우로 총 5번까지 수행가능하다. 따라서 최종적으로 5x5의 activation map을 얻게된다.

-
Stride = 2
stride가 2인 경우, output은 3x3이 된다.

-
Stride = 3
그렇다면, stride가 3인 경우는 어떨까? 다음과 같이 이미지에 필터가 정확히 맞아떨어지지 않는다. 이럴경우, 불균형한 결과를 초래할 수 있으므로 이러한 stride는 피하는 것이 좋다.

2-1-5) Spatial Dimension
위와 같은 이유로, 미리 output activation map의 사이즈를 계산하여, 정수로 나누어 떨어지는 stride를 사용하여야 한다. output의 size를 계산하는 공식은 다음과 같다.
\[let) \quad N=이미지 사이즈, F=필터 사이즈\\\] \[ouptut \; size = \frac{N - F}{stride} + 1\]stride가 3인 경우는 정확히 정수로 떨어지지 않는 것을 확인할 수 있다.

2-1-6) 주로 사용하는 size
-
filter
보통 filter는 3x3, 5x5, 7x7을 많이 사용한다.
-
stride
주로 stride는 filter의 사이즈에 따라서 다음과 같이 준다.
- 3x3 : 1
- 5x5 : 2
- 7x7 : 3
-
filter의 개수
필터의 개수는 32, 64, 128, 512와 같은 2의 제곱수를 사용한다
2-2) padding (zero-padding)
2-1-5에서 보았듯이, 특정한 stride를 사용하고 싶은데, filter가 이미지 가장자리까지 닿지 않는 경우에는 어떻게 하는 것이 좋을까? 그럴때는 padding이라는 기법을 사용하면 된다. padding은 이미지의 가장자리에 특정한 값을 채워넣는 기법인데, 이미지의 가장자리에 0을 채워 넣는 zero-padding을 일반적으로 많이 사용한다(mirror나 extend 등도 있음). padding을 사용하면, 모서리가 상대적으로 필터에 덜 적용되는 것을 막을 수 있으며, 위 상황처럼 필터가 가장자리까지 닿지 않는 경우의 문제도 해결할 수 있다. 또한, layer를 거치면서 입력 사이즈가 점점 줄어들게 되는데, padding을 하면 출력 사이즈와 입력 사이즈를 동일하게 유지할 수 있게된다. 만약 layer가 여러겹 쌓였는데 zero-padding을 하지 않으면, layer를 거칠수록 activation map은 점점 줄어들어 엄청 작아지게 되어 일부 정보가 손실될 우려가 있다.


2-2-1) Spatial Dimension
padding을 하게 되면 각 모서리마다 2개의 픽셀이 증가되므로, output size는 다음과 같다.
\[let) \quad N=이미지 사이즈, F=필터 사이즈\\\] \[ouptut \; size = \frac{N+2 - F}{stride} + 1\]2-3) 계층적 학습
각 layer는 여러개의 필터를 가지고 있으며, 각 필터마다 각각의 출력 map을 만드는데, 여러 layer를 쌓다보면 결국 각 필터들이 계층적으로 학습하게 되는 것을 알 수 있다. 다음은 이미지가 어떻게 생겨야 해당 뉴련의 활성을 최대화시킬 수 있는지를 시각화한 것이다(그리드의 각 요소는 각 뉴런의 활성을 최대화시키는 입력의 모양을 나타낸 것). 가령, 앞쪽에 있는 필터들은 edge와 같은 low-level feature를, mid-level을 보면 코너, blob등 좀 더 복잡한 특징을, high-level features를 보면 좀 더 객체와 닮은 것들이 출력으로 나온다.

각 conv의 입력은 이전 레이어에서 나온 edge maps이며, 이것들이 전부 누적되어 복잡한 추론을 하는 것이다. 그리고 이런 정보를 가지고 FC layer를 거치게 되면, 그 정보들을 한데 모아 클래스 스코어를 계산하는 것이다.
3. Pooling layer
Pooling은 activation map의 크기를 downsampling 하는 과정을 말한다. Conv layer에서 했던 것처럼, pooling에도 필터 크기와 stride를 정해 특정한 계산을 마치고, 슬라이딩 한다. 대신 Pooling은 conv layer와는 다르게, 기본적으로 영역이 겹치지 않게 하며 내적을 하는 것이 아니라 최대값을 찾는다(max pooling의 경우)
Convolutional Layer의 깊이가 깊어지면 많은 계산 양을 요구하는데, 이때 Pooling 기법을 이용해 이미지의 크기를 줄여, 연산 속도를 높일 수 있다(파라미터의 수가 줄기 때문). 이 때 중요한 점은, depth에는 아무런 변화도 일어나지 않고, 공간적으로만 줄어든다는 것이다. 가령, 224x224x64인 입력이 있다면 이를 112x112x64로 공간적으로 줄여줌(공간적인 불변성)
3-1) Max Pooling
다양한 종류의 Pooling 중, max pooling이 일반적으로 사용된다. max pooling은 지정된 filter 범위 내에서 가장 큰 값을 뽑아내고 stride만큼 슬라이딩 한다.

3-1-1) 단어 우월 효과
Max Pooling을 일반적으로 많이 사용하는 이유는, max pooling이 우리가 하는 인식과 상당부분 닮아있기 때문이다. 우리 뇌는 값들이 어떻게 분포하고 있는지 보다 그 값이 얼마나 큰지를 더 중요하게 여긴다. 그 예시로 단어 우월 효과를 들 수 있겠다. 우리는 단어의 앞 뒤 순서를 바꿔도 전체적인 형태가 유사하면 동일한 단어로 인식한다. 다음의 예문을 보도록 하자.
캠릿브지 대학의 연결구과에 따르면, 한 단어 안에서 글자가 어떤 순서로 배되열어 있는지는 중요하지 않고, 첫 번째와 마지막 글자가 올바른 위치에 있는 것이 중하요다고 한다. 나머지 글들자은 완전히 엉진망창의 순서로 되어 있라을지도 당신은 아무 문제 없이 이것을 읽을 수 있다. 왜하냐면, 인간의 두뇌는 모든 글자를 하하나나 읽는 것이 아니라 단어 하나를 전체로 인하식기 때이문다.
단어 앞뒤 순서가 뒤죽박죽으로 바뀌어도 쉽게 알아차릴 수가 없다. 사람이 단어를 인식할 때 개별 문자의 집합으로 인식하는 게 아닌 단어의 총체적 이미지로 인식하기 때문이라고 한다. max pooling도 이러한 사람의 인지 과정과 상당히 닮아있다. 우리가 다루는 값들은, 이 뉴런이 얼마나 활성되었는지, 바꿔 말하면 필터가 각 위치에서 얼마나 활성되었는지를 나타내는 값이다. 따라서 max pooling은 그 지역이 어디든 어떤 신호에 대해 얼마나 그 필터가 활성화되었는지를 알려준다고 알 수 있다.
따라서 이러한 이유로 max pooling을 많이 사용한다.
3-2) Spatial Dimension
앞서 conv layer에서 사용했던 수식을 그대로 이용해서 design choice를 할 수 있다
\[let) \quad N=이미지 사이즈, F=필터 사이즈\\\] \[ouptut \; size = \frac{N+2 - F}{stride} + 1\]여기서, 한 가지 특징이 있다면 pooling layer에서는 보통 padding을 하지 않는다. pooling을 하는 이유는 downsampling을 하고 싶기 때문인데, padding을 하면 이미지의 크기가 유지된다. 또한, conv layer처럼 코너의 값을 계산하지 못하는 경우가 pooling layer에서는 존재하지 않는다. 따라서 pooling 할때 padding은 고려하지 않아도 된다.
3-3) 주로 사용하는 size
가장 널리 쓰이는 필터 사이즈는 2x2, 3x3이고 보통 stride는 2로 한다. filter가 3x3일때도 보통 stride는 2x2로 하는 편이다.
3-4) pooling vs stride
우선, image를 다운 샘플링한다는 점에서 conv layer의 stride와 pooling layer는 비슷하다. 따라서 요즘에는 downsample할 떄 pooling보다 strdie를 더 많이 사용하고 있는 추세이다. 실제로 요즘은 stride가 더 좋은 성능을 보이고 있으며, pooling도 일종의 stride의 기법이라고 생각하면 된다. 상황에 맞게 선택하면 될 것 같다.
-
수정사항
관련 자료를 찾아보던 중, pooling이 stride보다 더 좋은 효율을 나타낸다는 글을 보았다. CS231n에서는 그 반대로 말하던데 어떤 말이 맞는지는 잘 모르겠다.
3. 예시
- ex1)
32x32x3의 input 이미지, 10개의 5x5필터, stride 1, padding 2일때의 출력 사이즈는? 32x32x10
f:32 padding:2x2 filter_size:-5 stride:/1 이므로 {(32+2x2-5)/1} + 1 = 32 -> 32x32 전체 필터의 갯수는 10개이므로 32x32x10의 activation map이 나옴
- ex2)
input volume : 32x32x3 filter : 10개의 5*5 필터가 있을때, 파라미터의 개수는 몇개일까?
5*5 필터가 입력의 depth만큼 통과 + bias 5x5x3 + 1(bias) = 76 따라서, 필터당 76개의 파라미터가 들어있는데,
그게 10개 있음 76*10 = 760개
4. 정리
CNN은 기본적으로 conv layer와 pool layer를 쌓아올리다가 마지막에 FC layer에 모아준다.
전형적인 CNN 아키텍쳐는 conv layer와 relu를 n번(일반적으로 n은 5정도) 반복하고, 그 중간에 pooling도 몇 번 들어간다. 그리고 fc layer에 연산결과를 모아주는데, 한번에서 두번 또는 그 이상일 수도 있다. 그리고 clas score를 구하기 위해 softmax를 사용한다.
댓글남기기